【理論】令和1年 問16|対称三相RLC負荷回路における電源電流および有効電力の計算問題
図のように線間電圧 \( 200 \) [V],周波数 \( 50 \) [Hz] の対称三相交流電源に \( \mathrm{RLC} \) 負荷が接続されている。
\( R = 10 \ \Omega \),電源角周波数を \( \omega \) [rad/s] として,\( \omega L = 10 \ \Omega \),\( \displaystyle \frac{1}{\omega C} = 20 \ \Omega \) である。
次の (a) および (b) の問いに答えよ。
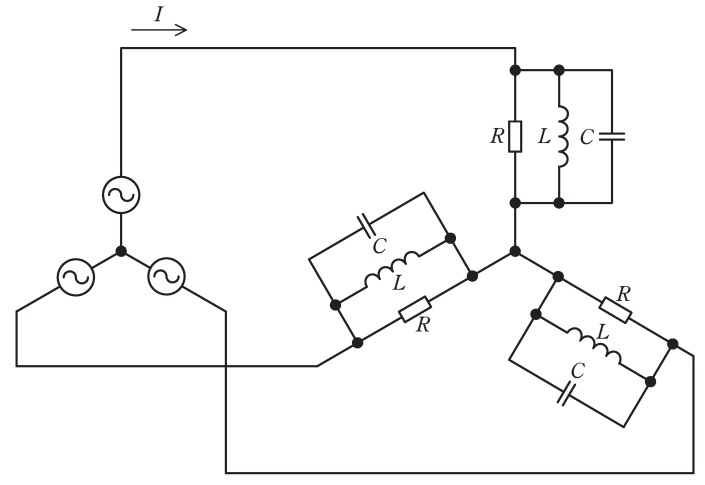
(a) 電源電流 \( I \) の値 [A] として,最も近いものを次の (1)~(5) のうちから一つ選べ。
(b) 三相負荷の有効電力の値 [\( \mathrm{kW} \)] として,最も近いものを次の (1)~(5) のうちから一つ選べ。
合格への方程式
三相対称交流回路の基本概念
三相対称交流回路は、位相が120°ずつずれた3つの正弦波電圧(または電流)からなる電力系統です。産業用電力供給の標準となっており、単相システムに比べて多くの利点があります。
三相対称交流回路の特徴
- 瞬時電力が一定(パルセーションがない)
- 同じ導体サイズで単相の1.5倍の電力伝送が可能
- 回転磁界の発生が容易(電動機への応用)
- Y結線とΔ結線の2種類の接続方式がある
三相電圧と電流の表現
三相対称交流回路の電圧と電流は、以下のように表現できます:
\[ \begin{aligned} v_a(t) &= V_m \sin(\omega t) \\[10pt] v_b(t) &= V_m \sin\left(\omega t - \frac{2\pi}{3}\right) \\[10pt] v_c(t) &= V_m \sin\left(\omega t - \frac{4\pi}{3}\right) \\[10pt] \end{aligned} \]
ここで、\(V_m\)は電圧の最大値、\(\omega = 2\pi f\)は角周波数です。
フェーザ表現
交流回路の解析では、時間領域の正弦波よりもフェーザ表現を用いることが一般的です。フェーザは複素数で表され、振幅と位相情報を持っています。
\[ \begin{aligned} \dot{V}_a &= V\angle 0° \\[10pt] \dot{V}_b &= V\angle -120° \\[10pt] \dot{V}_c &= V\angle -240° \\[10pt] \end{aligned} \]
ここで、\(V\)は実効値、\(\dot{V}\)はフェーザを表します。
Y結線とΔ結線
Y結線とΔ結線の比較
相電圧と線間電圧の関係
Y(スター)結線: \(V_L = \sqrt{3}V_P\)
Δ(デルタ)結線: \(V_L = V_P\)
相電流と線電流の関係
Y(スター)結線: \(I_L = I_P\)
Δ(デルタ)結線: \(I_L = \sqrt{3}I_P\)
中性点
Y(スター)結線: あり
Δ(デルタ)結線: なし
主な用途
Y(スター)結線: 電源側、高電圧機器
Δ(デルタ)結線: 負荷側、低電圧機器
注意点
三相対称交流回路の解析では、負荷が平衡(各相の負荷が等しい)であることを前提とすることが多いですが、実際のシステムでは不平衡が生じる場合があります。不平衡負荷の場合は、対称座標法などのより高度な解析手法が必要となります。
リアクタンスと複素インピーダンス
コイル(インダクタンス)のリアクタンス
インダクタンスが\(L \; [\mathrm{H}]\)のコイルを周波数\(f \; [\mathrm{Hz}]\)の交流電源に接続した時のリアクタンス\(X_L \; [\Omega]\)は次のように表されます:
\[ \begin{aligned} \mathrm{j}X_L &= \mathrm{j}\omega L \\[10pt] &= \mathrm{j}2\pi f L \\[10pt] \end{aligned} \]
ここで、\(\mathrm{j}\)は虚数単位、\(\omega = 2\pi f\)は角周波数です。
コイルの特性
- 電流に対して電圧が90°進む
- 周波数に比例してリアクタンスが増加
- 直流では短絡(\(X_L = 0\))、高周波では開放に近づく
コンデンサのリアクタンス
静電容量が\(C \; [\mathrm{F}]\)のコンデンサを周波数\(f \; [\mathrm{Hz}]\)の交流電源に接続した時のリアクタンス\(X_C \; [\Omega]\)は次のように表されます:
\[ \begin{aligned} -\mathrm{j}X_C &= \frac{1}{\mathrm{j}\omega C} \\[10pt] &= \frac{1}{\mathrm{j}2\pi f C} \\[10pt] \end{aligned} \]
\(\frac{1}{\mathrm{j}}\)と\(-\mathrm{j}\)の等価性
\[ \begin{aligned} \frac{1}{\mathrm{j}} &= \frac{1}{\mathrm{j}} \times \frac{\mathrm{j}}{\mathrm{j}} \\[10pt] &= \frac{\mathrm{j}}{\mathrm{j}^2} \\[10pt] &= \frac{\mathrm{j}}{-1} \\[10pt] &= -\mathrm{j} \\[10pt] \end{aligned} \]
このように、\(\frac{1}{\mathrm{j}}\)と\(-\mathrm{j}\)は数学的に同じ値です。
コンデンサの特性
- 電流に対して電圧が90°遅れる
- 周波数に反比例してリアクタンスが減少
- 直流では開放(\(X_C = \infty\))、高周波では短絡に近づく
複素インピーダンスの概念
交流回路では、抵抗\(R\)とリアクタンス\(X\)を合わせて複素インピーダンス\(Z\)として表現します:
\[ \begin{aligned} Z &= R + \mathrm{j}X \\[10pt] |Z| &= \sqrt{R^2 + X^2} \\[10pt] \phi &= \tan^{-1}\left(\frac{X}{R}\right) \\[10pt] \end{aligned} \]
ここで、\(|Z|\)はインピーダンスの大きさ、\(\phi\)は位相角です。
例題:リアクタンスの計算
周波数50Hzの電源に接続された100mHのコイルと50μFのコンデンサのリアクタンスを求めよ。
解答:
コイルのリアクタンス:
\[ \begin{aligned} X_L &= 2\pi f L \\[10pt] &= 2\pi \times 50 \times 0.1 \\[10pt] &= 31.4 \; [\Omega] \\[10pt] \end{aligned} \]
コンデンサのリアクタンス:
\[ \begin{aligned} X_C &= \frac{1}{2\pi f C} \\[10pt] &= \frac{1}{2\pi \times 50 \times 50 \times 10^{-6}} \\[10pt] &= 63.7 \; [\Omega] \\[10pt] \end{aligned} \]
RLC並列回路の特性
RLC並列回路の構成
RLC並列回路は、抵抗\(R\)、インダクタンス\(L\)、キャパシタンス\(C\)が並列に接続された回路です。三相システムでは、各相ごとにこのRLC並列回路が接続されます。
並列回路の特徴
- 各素子に同じ電圧が印加される
- 全体の電流は各素子の電流の和となる
- アドミタンス(インピーダンスの逆数)で計算すると便利
並列回路のインピーダンスとアドミタンス
RLC並列回路の合成インピーダンス\(Z_p\)は、各素子のインピーダンスの逆数の和の逆数として計算されます:
\[ \begin{aligned} \frac{1}{Z_p} &= \frac{1}{R} + \frac{1}{\mathrm{j}X_L} + \frac{1}{-\mathrm{j}X_C} \\[10pt] &= \frac{1}{R} + \frac{1}{\mathrm{j}X_L} - \frac{\mathrm{j}}{X_C} \\[10pt] \end{aligned} \]
アドミタンス\(Y\)を使うと、以下のように表せます:
\[ \begin{aligned} Y &= \frac{1}{Z} = G + \mathrm{j}B \\[10pt] Y_p &= \frac{1}{R} + \frac{1}{\mathrm{j}X_L} - \frac{\mathrm{j}}{X_C} \\[10pt] &= G + \mathrm{j}\left(B_C - B_L\right) \\[10pt] \end{aligned} \]
ここで、\(G = \frac{1}{R}\)はコンダクタンス、\(B_L = \frac{1}{X_L}\)はインダクティブサセプタンス、\(B_C = \frac{1}{X_C}\)はキャパシティブサセプタンスです。
並列共振
並列RLC回路では、\(B_L = B_C\)となる周波数で並列共振が発生します。この時、合成アドミタンスのサセプタンス成分が0となり、回路は純抵抗性となります。
\[ \begin{aligned} \omega_0 = \frac{1}{\sqrt{LC}} \\[10pt] \end{aligned} \]
ここで、\(\omega_0\)は共振角周波数です。
電流と力率の関係
RLC並列回路における各素子の電流:
\[ \begin{aligned} I_R &= \frac{V}{R} \\[10pt] I_L &= \frac{V}{\mathrm{j}X_L} = -\mathrm{j}\frac{V}{X_L} \\[10pt] I_C &= \frac{V}{-\mathrm{j}X_C} = \mathrm{j}\frac{V}{X_C} \\[10pt] \end{aligned} \]
合成電流\(I\)は:
\[ \begin{aligned} I &= I_R + I_L + I_C \\[10pt] &= \frac{V}{R} - \mathrm{j}\frac{V}{X_L} + \mathrm{j}\frac{V}{X_C} \\[10pt] &= \frac{V}{R} + \mathrm{j}V\left(\frac{1}{X_C} - \frac{1}{X_L}\right) \\[10pt] \end{aligned} \]
力率\(\cos\phi\)は:
\[ \begin{aligned} \cos\phi &= \frac{I_R}{|I|} = \frac{\frac{V}{R}}{\sqrt{\left(\frac{V}{R}\right)^2 + \left[V\left(\frac{1}{X_C} - \frac{1}{X_L}\right)\right]^2}} \\[10pt] &= \frac{1}{\sqrt{1 + \left[R\left(\frac{1}{X_C} - \frac{1}{X_L}\right)\right]^2}} \\[10pt] \end{aligned} \]
例題:RLC並列回路の解析
100V、50Hzの電源に、抵抗20Ω、インダクタンス100mH、キャパシタンス50μFの並列回路が接続されている。合成インピーダンス、電流、力率を求めよ。
解答:
各リアクタンスを計算します:
\[ \begin{aligned} X_L &= 2\pi f L = 2\pi \times 50 \times 0.1 = 31.4 \; [\Omega] \\[10pt] X_C &= \frac{1}{2\pi f C} = \frac{1}{2\pi \times 50 \times 50 \times 10^{-6}} = 63.7 \; [\Omega] \\[10pt] \end{aligned} \]
各素子の電流:
\[ \begin{aligned} I_R &= \frac{V}{R} = \frac{100}{20} = 5 \; [\mathrm{A}] \\[10pt] I_L &= \frac{V}{X_L} = \frac{100}{31.4} = 3.18 \; [\mathrm{A}] \; (\text{電圧より90°遅れ}) \\[10pt] I_C &= \frac{V}{X_C} = \frac{100}{63.7} = 1.57 \; [\mathrm{A}] \; (\text{電圧より90°進み}) \\[10pt] \end{aligned} \]
合成電流の計算(実部と虚部に分けて):
\[ \begin{aligned} I &= I_R + (I_C - I_L)\angle 90° \\[10pt] &= 5 + (1.57 - 3.18)\angle 90° \\[10pt] &= 5 - 1.61\mathrm{j} \\[10pt] |I| &= \sqrt{5^2 + (-1.61)^2} = \sqrt{25 + 2.59} = 5.24 \; [\mathrm{A}] \\[10pt] \end{aligned} \]
力率:
\[ \begin{aligned} \cos\phi &= \frac{I_R}{|I|} = \frac{5}{5.24} = 0.95 \; (\text{遅れ}) \\[10pt] \end{aligned} \]
合成インピーダンス:
\[ \begin{aligned} Z &= \frac{V}{I} = \frac{100}{5 - 1.61\mathrm{j}} \\[10pt] &= \frac{100(5 + 1.61\mathrm{j})}{(5 - 1.61\mathrm{j})(5 + 1.61\mathrm{j})} \\[10pt] &= \frac{500 + 161\mathrm{j}}{25 + 2.59} \\[10pt] &= \frac{500 + 161\mathrm{j}}{27.59} \\[10pt] &= 18.12 + 5.84\mathrm{j} \; [\Omega] \\[10pt] |Z| &= \sqrt{18.12^2 + 5.84^2} = 19.1 \; [\Omega] \\[10pt] \end{aligned} \]
三相平衡負荷の電力計算
三相電力の基本概念
三相平衡負荷における電力は、有効電力\(P\)、無効電力\(Q\)、皮相電力\(S\)の3つの要素で表されます。
三相平衡負荷の有効電力
有効電力は抵抗成分によって消費される実際の仕事をする電力です。一相あたりの有効電力\(P_1\)は:
\[ \begin{aligned} P_1 &= RI^2 \\[10pt] &= \frac{V^2}{R} \\[10pt] \end{aligned} \]
三相負荷の合計有効電力\(P_3\)は:
\[ \begin{aligned} P_3 &= 3P_1 \\[10pt] \end{aligned} \]
無効電力と皮相電力
無効電力\(Q\)は、リアクタンス成分によって消費される電力で、実際の仕事はしませんが、電力系統内を行き来します。
一相あたりの無効電力\(Q_1\):
\[ \begin{aligned} Q_1 &= X_L I^2 - X_C I^2 \\[10pt] &= (X_L - X_C) I^2 \\[10pt] &= X I^2 \\[10pt] \end{aligned} \]
三相の無効電力\(Q_3\):
\[ \begin{aligned} Q_3 &= 3Q_1 \\[10pt] \end{aligned} \]
三相の皮相電力\(S_3\):
\[ \begin{aligned} S_3 &= \sqrt{P_3^2 + Q_3^2} \\[10pt] &= 3VI \; \text{(Y結線の場合)} \\[10pt] &= \sqrt{3}V_LI_L \; \text{(Y結線もΔ結線も共通)} \\[10pt] \end{aligned} \]
力率と電力の関係
力率\(\cos\phi\)は、皮相電力に対する有効電力の比率です:
\[ \begin{aligned} \cos\phi &= \frac{P_3}{S_3} \\[10pt] P_3 &= S_3 \cos\phi \\[10pt] Q_3 &= S_3 \sin\phi \\[10pt] \end{aligned} \]
三相電力の測定方法
三相平衡負荷の電力測定には、以下の方法があります:
| 測定方法 | 説明 | 計算式 |
|---|---|---|
| 三電力計法 | 各相の電力を個別に測定 | \(P_3 = P_a + P_b + P_c\) |
| 二電力計法 | 二つの電力計で三相電力を測定 | \(P_3 = P_1 + P_2\) |
| 一電力計法 | 平衡負荷の一相の電力を測定し3倍 | \(P_3 = 3P_1\) |
例題:三相RLC並列負荷の電力計算
200V(線間電圧)、50Hz、三相平衡Y結線の電源に、各相に抵抗50Ω、インダクタンス100mH、キャパシタンス40μFが並列に接続されている。全体の有効電力、無効電力、皮相電力、力率を求めよ。
解答:
Y結線の場合、相電圧は:
\[ \begin{aligned} V_P &= \frac{V_L}{\sqrt{3}} = \frac{200}{\sqrt{3}} = 115.5 \; [\mathrm{V}] \\[10pt] \end{aligned} \]
リアクタンスの計算:
\[ \begin{aligned} X_L &= 2\pi f L = 2\pi \times 50 \times 0.1 = 31.4 \; [\Omega] \\[10pt] X_C &= \frac{1}{2\pi f C} = \frac{1}{2\pi \times 50 \times 40 \times 10^{-6}} = 79.6 \; [\Omega] \\[10pt] \end{aligned} \]
各素子の電流(一相あたり):
\[ \begin{aligned} I_R &= \frac{V_P}{R} = \frac{115.5}{50} = 2.31 \; [\mathrm{A}] \\[10pt] I_L &= \frac{V_P}{X_L} = \frac{115.5}{31.4} = 3.68 \; [\mathrm{A}] \\[10pt] I_C &= \frac{V_P}{X_C} = \frac{115.5}{79.6} = 1.45 \; [\mathrm{A}] \\[10pt] \end{aligned} \]
一相あたりの有効電力:
\[ \begin{aligned} P_1 &= V_P I_R = 115.5 \times 2.31 = 266.8 \; [\mathrm{W}] \\[10pt] \end{aligned} \]
三相の有効電力:
\[ \begin{aligned} P_3 &= 3P_1 = 3 \times 266.8 = 800.4 \; [\mathrm{W}] \\[10pt] \end{aligned} \]
一相あたりの無効電力(インダクティブが正、キャパシティブが負):
\[ \begin{aligned} Q_{1L} &= V_P I_L = 115.5 \times 3.68 = 425.0 \; [\mathrm{var}] \; \text{(遅れ)} \\[10pt] Q_{1C} &= -V_P I_C = -115.5 \times 1.45 = -167.5 \; [\mathrm{var}] \; \text{(進み)} \\[10pt] Q_1 &= Q_{1L} + Q_{1C} = 425.0 + (-167.5) = 257.5 \; [\mathrm{var}] \; \text{(正味遅れ)} \\[10pt] \end{aligned} \]
三相の無効電力:
\[ \begin{aligned} Q_3 &= 3Q_1 = 3 \times 257.5 = 772.5 \; [\mathrm{var}] \\[10pt] \end{aligned} \]
三相の皮相電力:
\[ \begin{aligned} S_3 &= \sqrt{P_3^2 + Q_3^2} \\[10pt] &= \sqrt{800.4^2 + 772.5^2} \\[10pt] &= \sqrt{640,640 + 596,756} \\[10pt] &= \sqrt{1,237,396} \\[10pt] &= 1,112 \; [\mathrm{VA}] \\[10pt] \end{aligned} \]
力率:
\[ \begin{aligned} \cos\phi &= \frac{P_3}{S_3} = \frac{800.4}{1,112} = 0.72 \; \text{(遅れ)} \\[10pt] \end{aligned} \]
力率改善と共振
力率改善の必要性
工場や産業設備では、モータなどの誘導性負荷が多く使用されるため、力率が遅れ(低力率)になりがちです。低力率は以下の問題を引き起こします:
- 電力系統の送電容量の低下
- 電圧降下の増加
- 送電損失の増加
- 電力料金の割増(多くの電力会社は低力率に対しペナルティを課す)
力率改善の方法
力率改善の最も一般的な方法は、適切な容量のコンデンサを並列に接続することです。これにより、誘導性負荷(モータなど)の遅れ無効電力を打ち消し、力率を向上させることができます。
必要なコンデンサ容量の計算
力率を\(\cos\phi_1\)から\(\cos\phi_2\)に改善するために必要なコンデンサの容量(キャパシタンス)は次のように計算できます:
\[ \begin{aligned} Q_C &= P(\tan\phi_1 - \tan\phi_2) \\[10pt] X_C &= \frac{V^2}{Q_C} \\[10pt] C &= \frac{1}{2\pi f X_C} \\[10pt] \end{aligned} \]
ここで、\(P\)は有効電力、\(V\)は電圧、\(f\)は周波数です。
例題:力率改善の計算
200V(線間電圧)、50Hz、三相平衡Y結線の負荷で、有効電力が10kW、力率が0.7(遅れ)である。力率を0.95(遅れ)まで改善するために必要なコンデンサの容量を求めよ。
解答:
現在の力率角と目標の力率角:
\[ \begin{aligned} \phi_1 &= \cos^{-1}(0.7) = 45.6° \\[10pt] \phi_2 &= \cos^{-1}(0.95) = 18.2° \\[10pt] \end{aligned} \]
必要なコンデンサの無効電力:
\[ \begin{aligned} Q_C &= P(\tan\phi_1 - \tan\phi_2) \\[10pt] &= 10,000 \times (\tan 45.6° - \tan 18.2°) \\[10pt] &= 10,000 \times (1.02 - 0.33) \\[10pt] &= 10,000 \times 0.69 \\[10pt] &= 6,900 \; [\mathrm{var}] \\[10pt] \end{aligned} \]
Y結線での相電圧:
\[ \begin{aligned} V_P &= \frac{V_L}{\sqrt{3}} = \frac{200}{\sqrt{3}} = 115.5 \; [\mathrm{V}] \\[10pt] \end{aligned} \]
各相に必要なコンデンサの無効電力:
\[ \begin{aligned} Q_{C1} &= \frac{Q_C}{3} = \frac{6,900}{3} = 2,300 \; [\mathrm{var}] \\[10pt] \end{aligned} \]
各相のコンデンサのリアクタンス:
\[ \begin{aligned} X_C &= \frac{V_P^2}{Q_{C1}} = \frac{115.5^2}{2,300} = 5.8 \; [\Omega] \\[10pt] \end{aligned} \]
各相に必要なキャパシタンス:
\[ \begin{aligned} C &= \frac{1}{2\pi f X_C} = \frac{1}{2\pi \times 50 \times 5.8} = 549 \; [\mu\mathrm{F}] \\[10pt] \end{aligned} \]
よって、Y結線で各相に549μFのコンデンサを接続するか、Δ結線で各相に183μF(=549μF/3)のコンデンサを接続すれば良いことになります。
並列共振と直列共振
RLC回路では、インダクタンスとキャパシタンスの相互作用により共振現象が発生する場合があります。共振には並列共振と直列共振の2種類があります。
| 特性 | 並列共振 | 直列共振 |
|---|---|---|
| インピーダンス | 最大 | 最小 |
| 電流 | 最小 | 最大 |
| 共振条件 | \(B_L = B_C\) | \(X_L = X_C\) |
| 共振周波数 | \(\omega_0 = \frac{1}{\sqrt{LC}}\) | \(\omega_0 = \frac{1}{\sqrt{LC}}\) |
| 応用例 | フィルタ回路、発振回路 | 同調回路、周波数選択回路 |
共振の利用と注意点
共振現象は、特定の周波数を選択する回路や発振回路などに積極的に利用されます。一方で、電力系統では意図しない共振(特に高調波との共振)が過電圧や過電流を引き起こす危険性があるため、注意が必要です。
電力系統における共振の危険性
電力系統に力率改善用のコンデンサを設置する場合、特に高調波が存在する環境では、システム全体のインピーダンス特性を考慮して、意図しない共振が発生しないよう設計する必要があります。必要に応じて、直列リアクトルを追加するなどの対策が取られます。
例題:共振周波数の計算
100mHのインダクタンスと40μFのキャパシタンスからなる回路の共振周波数を求めよ。
解答:
\[ \begin{aligned} f_0 &= \frac{1}{2\pi\sqrt{LC}} \\[10pt] &= \frac{1}{2\pi\sqrt{0.1 \times 40 \times 10^{-6}}} \\[10pt] &= \frac{1}{2\pi\sqrt{4 \times 10^{-6}}} \\[10pt] &= \frac{1}{2\pi \times 2 \times 10^{-3}} \\[10pt] &= \frac{1}{4\pi \times 10^{-3}} \\[10pt] &= \frac{10^3}{4\pi} \\[10pt] &= 79.6 \; [\mathrm{Hz}] \\[10pt] \end{aligned} \]
この周波数では、回路のインピーダンス特性が大きく変化します。直列回路ではインピーダンスが最小になり、並列回路ではインピーダンスが最大になります。
🔍 ワンポイントアドバイス: 三相RLC並列回路を解析する際は、まず各素子のリアクタンスを計算し、次に各素子の電流を求めることがポイントです。また、力率改善の計算では「\(\tan\phi_1 - \tan\phi_2\)」の値を覚えておくと便利です。例えば、力率0.7から0.9への改善では約0.5、0.8から0.95への改善では約0.4の値となります。第3種電気主任技術者試験では、このような力率改善の計算問題がよく出題されます。実務上は、力率改善によるコスト削減効果と設備投資のバランスを考慮することも重要です。
今日は三相平衡負荷の計算をするで!まずは問題を見てみよか。
下の図は三相平衡負荷の1相分の等価回路や。この回路は抵抗R、インダクタンスL、コンデンサCが並列に接続されとるんや。
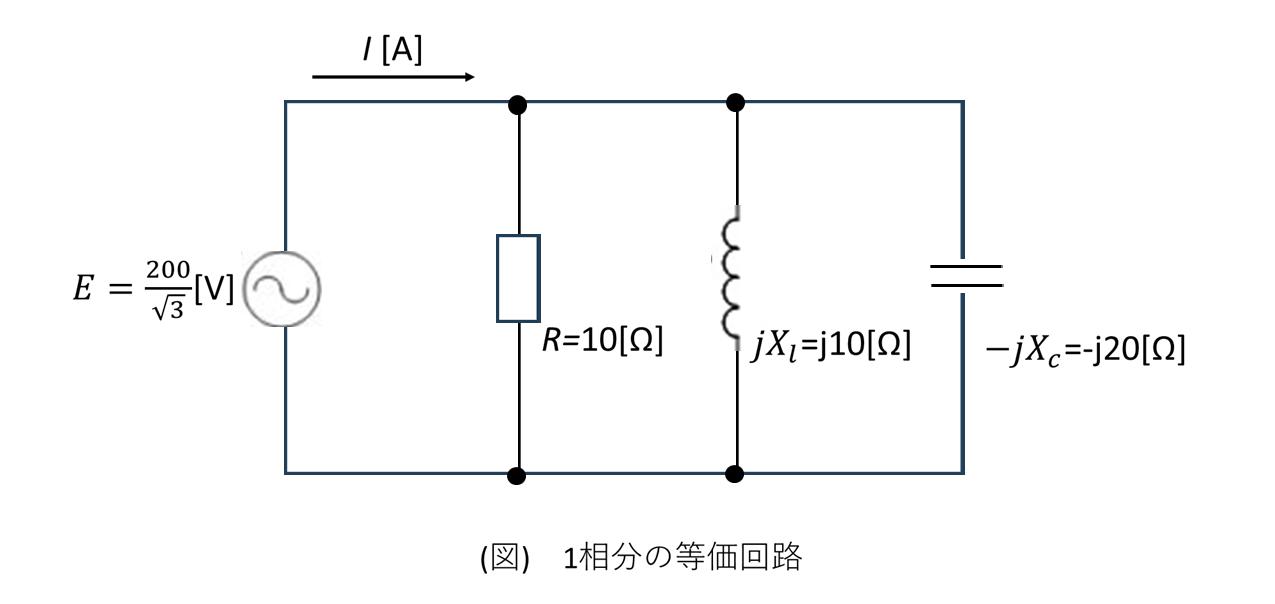
条件として、線間電圧が200V、抵抗値R=10Ω、インダクタンスのリアクタンスXL=10Ω、コンデンサのリアクタンスXC=20Ωやて。
まずは(a)問題や。この回路で電源に流れる電流の実効値を求めてみよか。どう考える?
三相平衡負荷の計算をするには、まず1相あたりの計算を行い、それを三相に拡張すればよいと思います。
まず、1相あたりの相電圧を求めます。線間電圧が200Vなので、相電圧は:
\( V_{相} = \frac{200}{\sqrt{3}} \) V
次に、各素子に流れる電流を計算します。並列回路なので、各素子には同じ電圧がかかります。
そうやな、まず相電圧を求めるのが大事や。線間電圧が200Vやから、相電圧は \( \frac{200}{\sqrt{3}} \) Vになるな。
各素子に流れる電流を求めていこか。まずは抵抗Rに流れる電流 \( \dot{I}_R \) はどうなる?
抵抗Rに流れる電流は、オームの法則より:
\[ \begin{aligned} \dot{I}_R &= \frac{V_{相}}{R} \\[10pt] &= \frac{\frac{200}{\sqrt{3}}}{10} \\[10pt] &= \frac{20}{\sqrt{3}} \ \mathrm{[A]} \end{aligned} \]この電流は抵抗に流れるので、位相は電圧と同相になります。
ええやん!次はインダクタンスに流れる電流 \( \dot{I}_L \) を求めてみよか。インダクタンスの場合、電流は電圧より遅れることに注意してな。
インダクタンスに流れる電流は、インピーダンスを考慮して:
\[ \begin{aligned} \dot{I}_L &= \frac{V_{相}}{jX_L} \\[10pt] &= \frac{\frac{200}{\sqrt{3}}}{j10} \\[10pt] &= -j\frac{20}{\sqrt{3}} \ \mathrm{[A]} \end{aligned} \]インダクタンスでは電流が電圧より90度遅れるため、-j成分として表されます。
よう理解できてるな!最後にコンデンサに流れる電流 \( \dot{I}_C \) も求めてみよか。コンデンサの場合は電流が電圧より進むことに注意してな。
コンデンサに流れる電流は、インピーダンスを考慮して:
\[ \begin{aligned} \dot{I}_C &= \frac{V_{相}}{-jX_C} \\[10pt] &= \frac{\frac{200}{\sqrt{3}}}{-j20} \\[10pt] &= j\frac{10}{\sqrt{3}} \ \mathrm{[A]} \end{aligned} \]コンデンサでは電流が電圧より90度進むため、j成分として表されます。また、コンデンサのリアクタンスは20Ωなので、インダクタンスより電流が小さくなることがわかります。
ええ感じや!それじゃあ、これらの電流を合成して、電源に流れる全電流 \( \dot{I} \) を求めてみよか。各素子は並列接続されているから、電流は足し合わせるんやで。
電源に流れる全電流は、各素子に流れる電流の和になります:
\[ \begin{aligned} \dot{I} &= \dot{I}_R + \dot{I}_L + \dot{I}_C \\[10pt] &= \frac{20}{\sqrt{3}} + (-j)\frac{20}{\sqrt{3}} + j\frac{10}{\sqrt{3}} \\[10pt] &= \frac{20}{\sqrt{3}} - j\frac{20}{\sqrt{3}} + j\frac{10}{\sqrt{3}} \\[10pt] &= \frac{20}{\sqrt{3}} - j\frac{10}{\sqrt{3}} \ \mathrm{[A]} \end{aligned} \]これは複素数表示の電流ですが、問題では実効値(大きさ)を求める必要があります。
そうや!複素数表示された電流の大きさ(実効値)を求めるには、実部と虚部の二乗和の平方根を計算すればええんや。計算してみよか。
電流の実効値を計算します:
\[ \begin{eqnarray} I &=& \sqrt{\left(\frac{20}{\sqrt{3}}\right)^2 + \left(\frac{10}{\sqrt{3}}\right)^2} \\[20pt] &=& \sqrt{\frac{400}{3} + \frac{100}{3}} \\[20pt] &=& \sqrt{\frac{500}{3}} \\[20pt] &\approx& 12.9 \ \mathrm{[A]} \\[20pt] &\approx& 13 \ \mathrm{[A]} \end{eqnarray} \]よって、電源に流れる電流の実効値は約13[A]となります。
これは選択肢の(3)に該当します。
正解や!電流の大きさは13Aということで、選択肢の(3)が正解やな。
次は(b)問題や。この三相平衡負荷の有効電力を求めてみよか。三相の有効電力はどう考えるのが良いかな?
三相平衡負荷の有効電力は、まず1相あたりの有効電力を求めてから、それを3倍すれば求められます。
有効電力は抵抗成分でのみ消費されるので、まず抵抗Rでの消費電力を計算します。
1相あたりの有効電力P₁は:
\[ \begin{eqnarray} P_1 &=& \frac{V_{相}^2}{R} \\[20pt] &=& \frac{\left(\frac{200}{\sqrt{3}}\right)^2}{10} \\[20pt] &=& \frac{40000/3}{10} \\[20pt] &=& \frac{4000}{3} \ \mathrm{[W]} \end{eqnarray} \]ここで注意すべきは、インダクタンスやコンデンサでは有効電力が消費されないということです。リアクタンス成分では無効電力のみが関与します。
そうやな!有効電力は抵抗成分でのみ消費されるから、1相あたりの有効電力は \( \frac{4000}{3} \) Wになるな。じゃあ、三相全体での有効電力はどうなる?
三相全体での有効電力P₃は、1相あたりの有効電力の3倍になります:
\[ \begin{eqnarray} P_3 &=& 3P_1 \\[20pt] &=& 3 \times \frac{4000}{3} \\[20pt] &=& 4000 \ \mathrm{[W]} \\[20pt] &=& 4 \ \mathrm{[kW]} \end{eqnarray} \]したがって、三相平衡負荷の有効電力は4[kW]となります。
これは選択肢の(4)に該当します。
素晴らしい!有効電力は4kWということで、選択肢の(4)が正解やな。
今回の問題で大事なポイントをまとめとこか。三相平衡負荷では:
1. 線間電圧から相電圧を求めるときは \( V_{相} = \frac{V_{線間}}{\sqrt{3}} \) を使う。
2. 並列回路では各素子に同じ電圧がかかるから、それぞれの特性に応じた電流計算をする。
3. 抵抗では電流と電圧は同相、インダクタンスでは電流が電圧より90度遅れ、コンデンサでは電流が電圧より90度進む。
4. 複素数表示の電流を合成するときは、実部同士、虚部同士を足し合わせる。
5. 有効電力は抵抗成分でのみ消費され、三相全体では1相あたりの3倍になる。
この問題の解き方、理解できたか?
はい、理解できました!三相平衡負荷の計算の流れとポイントがよくわかりました。
特に重要だと感じたのは:
・線間電圧と相電圧の関係(√3で割る)
・各素子(R、L、C)の電流の位相関係
・複素数表示での電流の合成方法
・有効電力の計算(抵抗成分のみを考慮する)
これらを押さえておけば、三相回路の問題に対応できそうです。また、複素数表示を使うことで、交流回路の計算が整理しやすくなることもよくわかりました。
ええ理解やな!電気主任技術者試験では、こうした三相回路の計算問題がよく出てくるからな。特に複素数を使った計算に慣れておくことが大事やで。
もし別のパターンの問題、例えばY結線やΔ結線の違いとか、力率改善のための計算とかも勉強したかったら、また言うてな。今日はお疲れさん!
はい、ありがとうございました先生!
今日は三相平衡負荷の計算について、特に複素数を使った電流計算と有効電力の求め方をしっかり学ぶことができました。
次回はY結線とΔ結線の違いや力率改善についても勉強してみたいです。電気主任技術者試験に向けて、様々なパターンの問題に対応できるよう頑張ります!
解説まとめ
■ 平衡三相回路の解析とは
平衡三相回路は電力系統や産業用機器で広く使用される基本的な回路構成です。三相回路は各相が電気的に対称(平衡)であるため、一相分の解析を行い、その結果を三相分に拡張することができます。これにより計算が簡略化され、効率的に回路の特性を把握することが可能になります。
■ 計算手順と公式
- リアクタンスの計算
コイルとコンデンサのリアクタンスを角周波数を用いて求めます。
\( X_{\mathrm{L}} = \omega L \)
\( X_{\mathrm{C}} = \frac{1}{\omega C} \)
- 一相等価回路の作成
リアクタンスを用いて一相分の等価回路を描きます。

- 各素子に流れる電流の計算
並列接続された各素子に流れる電流をオームの法則で求めます。
\( \dot{I}_{\mathrm{R}} = \frac{V_{\mathrm{P}}}{R} \)
\( \dot{I}_{\mathrm{L}} = \frac{V_{\mathrm{P}}}{jX_{\mathrm{L}}} \)
\( \dot{I}_{\mathrm{C}} = \frac{V_{\mathrm{P}}}{-jX_{\mathrm{C}}} \)
- 合成電流の計算
各素子に流れる電流のベクトル和から合成電流を求めます。
\( \dot{I} = \dot{I}_{\mathrm{R}} + \dot{I}_{\mathrm{L}} + \dot{I}_{\mathrm{C}} \)
- 電力の計算
抵抗成分のみが有効電力を消費するため、抵抗に関する計算を行います。
\( P_{1} = \frac{V_{\mathrm{P}}^2}{R} \)
\( P_{3} = 3P_{1} \)
■ 具体的な計算例
問題条件
- 三相平衡負荷(R, L, Cが並列接続)
- 三相線間電圧: \( V_{\mathrm{L}} = 200 \ \mathrm{[V]} \)
- 抵抗値: \( R = 10 \ \mathrm{[\Omega]} \)
- コイルのリアクタンス: \( X_{\mathrm{L}} = 10 \ \mathrm{[\Omega]} \)
- コンデンサのリアクタンス: \( X_{\mathrm{C}} = 20 \ \mathrm{[\Omega]} \)
(a) 電源に流れる電流の大きさの計算
\[ \begin{aligned} \text{まず相電圧を求めます} \\[5pt] V_{\mathrm{P}} &= \frac{V_{\mathrm{L}}}{\sqrt{3}} = \frac{200}{\sqrt{3}} \ \mathrm{[V]} \\[10pt] \text{各素子に流れる電流を計算します} \\[5pt] \dot{I}_{\mathrm{R}} &= \frac{V_{\mathrm{P}}}{R} = \frac{200/\sqrt{3}}{10} = \frac{20}{\sqrt{3}} \ \mathrm{[A]} \\[10pt] \dot{I}_{\mathrm{L}} &= \frac{V_{\mathrm{P}}}{j X_{\mathrm{L}}} = \frac{200/\sqrt{3}}{j10} = -j\frac{20}{\sqrt{3}} \ \mathrm{[A]} \\[10pt] \dot{I}_{\mathrm{C}} &= \frac{V_{\mathrm{P}}}{-j X_{\mathrm{C}}} = \frac{200/\sqrt{3}}{-j20} = j\frac{10}{\sqrt{3}} \ \mathrm{[A]} \\[10pt] \text{電源に流れる電流を求めます} \\[5pt] \dot{I} &= \dot{I}_{\mathrm{R}} + \dot{I}_{\mathrm{L}} + \dot{I}_{\mathrm{C}} \\[5pt] &= \frac{20}{\sqrt{3}} - j\frac{20}{\sqrt{3}} + j\frac{10}{\sqrt{3}} \\[5pt] &= \frac{20}{\sqrt{3}} - j\frac{10}{\sqrt{3}} \ \mathrm{[A]} \\[10pt] \text{電流の大きさを計算します} \\[5pt] I &= \sqrt{\left(\frac{20}{\sqrt{3}}\right)^2 + \left(\frac{10}{\sqrt{3}}\right)^2} \\[5pt] &= \sqrt{\frac{400}{3} + \frac{100}{3}} \\[5pt] &= \sqrt{\frac{500}{3}} \\[5pt] &\approx 12.9 \ \mathrm{[A]} \\[5pt] &\approx 13 \ \mathrm{[A]} \end{aligned} \]結論:電源に流れる電流の大きさは 13 [A] である。(解答:選択肢(3))
(b) 三相負荷の有効電力の計算
\[ \begin{aligned} \text{一相あたりの有効電力を計算します} \\[5pt] P_{1} &= \frac{V_{\mathrm{P}}^2}{R} \\[5pt] &= \frac{\left(200/\sqrt{3}\right)^2}{10} \\[5pt] &= \frac{40000/3}{10} \\[5pt] &= \frac{4000}{3} \ \mathrm{[W]} \\[10pt] \text{三相負荷の全有効電力を計算します} \\[5pt] P_{3} &= 3P_{1} \\[5pt] &= 3 \times \frac{4000}{3} \\[5pt] &= 4000 \ \mathrm{[W]} \\[5pt] &= 4 \ \mathrm{[kW]} \end{aligned} \]結論:三相負荷の有効電力は 4 [kW] である。(解答:選択肢(4))
■ 実務上の留意点
三相平衡回路の解析は電気設備の設計・運用で重要な役割を果たします。
- 平衡三相回路は一相分の解析で全体を把握できるため、設計や故障解析が簡略化されます。
- 力率改善用のコンデンサ容量を決定する際、リアクティブパワーのバランスを考慮することが重要です。
- 電流計算の際は、ベクトル量として計算するため、大きさだけでなく位相も考慮する必要があります。
- 実際の機器では、コイルに内部抵抗があることを考慮し、より詳細なモデル化が必要な場合があります。
- 電力計算では、無効電力も含めた皮相電力を考慮して、配線やブレーカーの容量を決定します。